Linguaggi regolari

Intro

Definizione: Automa a stati finiti (DFA)

Il piu semplice modello di computazione. Scorre l’input bit a bit in modo sequenziale “scorrendolo”

---

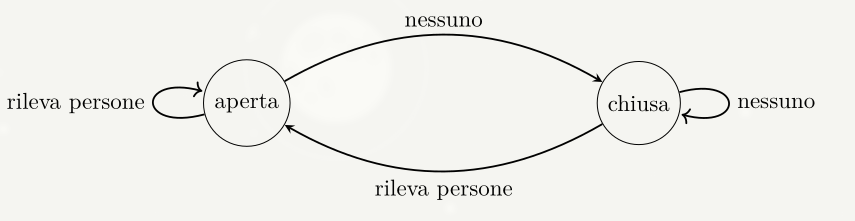
Esempio di un problema

Si vuole modellare una porta automatica con sensore che si apre quando qualcuno si trova nelle vicinanze:

/	Nessuno	Davanti	Dietro	Entrambi
Chiuso	Chiuso	Aperto	Aperto	Aperto
Aperto	Chiuso	Aperto	Aperto	Aperto

In questo caso un automa che rappresenta il seguente problema puo essere:

---

Automi

Un automa si presenta cosi:

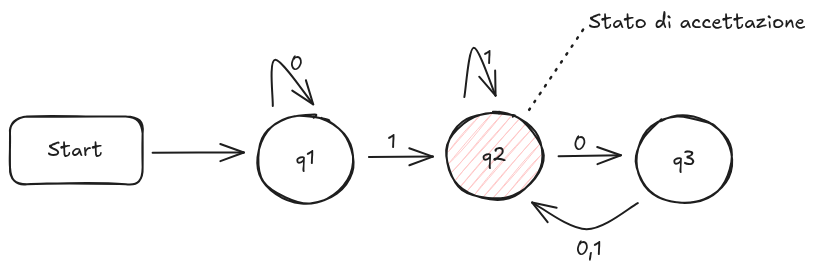
Dove: q1,q2,q3: sono STATI.

q2: e uno STATO DI ACCETTAZIONE.

→: si chiamano TRANSAZIONI.

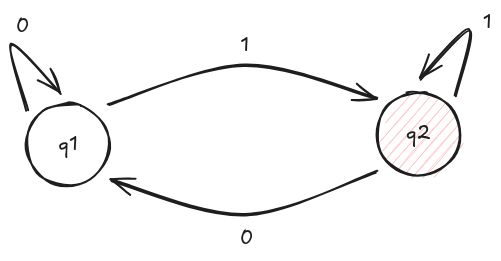
In questo caso questo automa accetta ad esempio la stringa 11101

Definizione: DFA

Un DFA (Deterministic Finite Automa) e una 5-tupla, (Q, Σ, δ, q0 , F ) di cui:

• Q: Insieme finito degli stati .
• Σ: L’alfabeto che compone le stringhe in input.
• δ: Funzione Q x Σ → Q.
• q0: Stato iniziale, q0 ∈ Q.
• F: F ⊆ Q Stati finali (accettazione).

---

Funzione di Transizione e Configurazione

Se M e un DFA l’insieme delle stringhe riconosciute da M si denota L(M) ovvero il linguaggio riconosciuto da M (Puo anche essere che L = Ø)

Per definire formalmente un linguaggio di un automa e necessario introdurre la funzione di transizione estesa. ${\delta }^{\ast }:Q\times {\Sigma }^{\ast }\to Q$

$$\{\begin{array}{ll}{\delta }^{\ast }(q,ϵ)& =\delta (q,ϵ)\\ {\delta }^{\ast }(q,ax)& ={\delta }^{\ast }(\delta (q,a),x)a\in \Sigma x\in {\Sigma }^{\ast }\end{array}$$

Un altro concetto utile e la Configurazione (coppia in Q x Σ*):

1. Lo Stato (corrente)
2. Cosa resta da leggere Dato x ∈ Σ*, la configurazione iniziale e (q0,x)

Passo Computazionale: porta da una configurazione ad un’altra rispettando le δ. Relazione Binaria: $(p,ax){⊢}_M(q,x)\iff \delta (p,a)=q$ dove p,q ∈ Q, a ∈ Σ, x ∈ Σ*.

Posso estendere ${⊢}_{M^{\ast }}$ considerando la chiusura riflessiva e transitiva:

1. $(q,x){⊢}_{M^{\ast }}(q,x)$ (riflessivita)
2. $(q,aby){⊢}_M(p,by),(p,by){⊢}_M(r,y)\Rightarrow (q,aby){⊢}_{M^{\ast }}(r,y)$ dove q,p,r ∈ Q; a,b ∈ Σ; y ∈ Σ*

---

DSF (Linguaggio Accettato)

Diciamo che x ∈ Σ* e accettato da M(Q, Σ, δ, q0 , F ) se

$${\delta }^{\ast }(q_0,x)\in Foppure(q_0,x){⊢}_{M^{\ast }}(q,ϵ)q\in F$$

Ricordiamo che ε e la stringa vuota. Da cui:

$$L(M)=\{x\in {\Sigma }^{\ast }:{\delta }^{\ast }(q_0,x)\in F\}$$

Esempio:

$$(q_1,011){⊢}_M(q_1,11){⊢}_M(q_2,1){⊢}_M(q_2,ϵ)$$ $${\delta }^{\ast }(q_1,011)=(q_2,ϵ)q_2\in Fw=011\in L(M)$$

---

Finally…

Ora possiamo dare la definizione formale dei Linguaggi Regolari:

Definizione: Linguaggi Regolari

$REG=\{L\subseteq {\Sigma }^{\ast }:\exists DFAMt.c.L(M)=L\}$

Vogliamo capire come progettare DFA per un dato linguaggio, facciamo un esempio:

$L=\{x\in \{0,1{\}}^{\ast }|x=1y,y\in \{0,1{\}}^{\ast }\}$

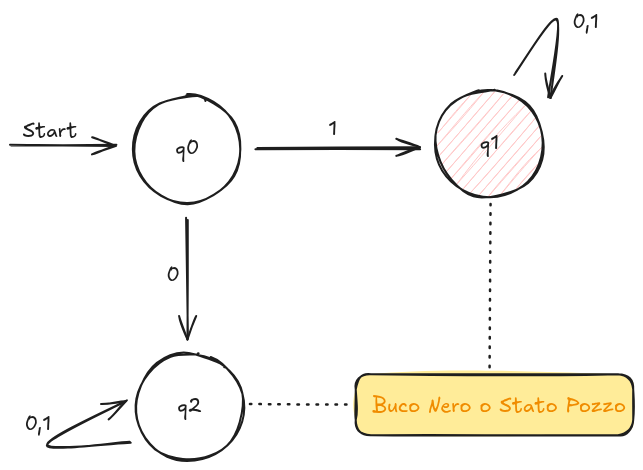
Dobbiamo eseguire una prova di correttezza:

DFA accetta $x\iff x\in L$ . Osserviamo che:

$$\begin{array}{c}{\delta }^{\ast }(q_1,u)=q_1\forall u\in \{0,1{\}}^{\ast }\\ {\delta }^{\ast }(q_2,u)=q_2\forall u\in \{0,1{\}}^{\ast }\end{array}$$

Per induzione dimostriamo che $x\in L\iff$ DFA accetta x:

Base: $|x|=0sex=ϵ,{\delta }^{\ast }(q_0,ϵ)=\delta (q_0,ϵ)=q_0\in F$ Induttivo: Sia $n\ge 0,|w|\le n$ supponiamo che:

$${\delta }^{\ast }(q_0,w)=\{\begin{array}{l}{q}_{0}sew=ϵ\\ q_{1}sewiniziacon1\\ q_{2}sewiniziacon0\end{array}$$

Prendo $xt.c.|x|=u+1$ e lo penso $x=au$ con $a\in \{0,1\},u\in \{0,1{\}}^n$ Da cui:

$${\delta }^{\ast }(q_0,x)={\delta }^{\ast }(q_0,au)={\delta }^{\ast }(\delta (q_0,a),u)$$

Due casi:

$$\begin{array}{r}\delta (q_0,a)=q_{2}sea=0\\ \delta (q_0,a)=q_{1}sea=1\end{array}$$

Abbiamo gia dimostrato che se entro in q1,q2 ci rimango . Con quest'ultimo passaggio abbiamo dimostrato che avendo una stringa u (che rappresenta qualsiasi combinazione binaria di lunghezza n) e un ultimo carattere a, in ogni caso, entriamo in q1,q2

Sui linguaggi possiamo effettuare Operazioni sui Linguaggi